Einer Gruppe von Heidelberger Physikern ist es gelungen, zum ersten Mal überhaupt sogenannte Pauli-Kristalle in einem Experiment zu beobachten. Ihre Ergebnisse haben sie Mitte Januar in Physical Review Letters veröffentlicht. Ein erstes Manuskript hatten sie bereits im Mai 2020 als Preprint auf dem arXiv hochgeladen. Was diese Pauli-Kristalle sind, warum sie spannend sind und wie die Experimentatoren sie beobachten konnten, möchte ich versuchen euch hier zu erklären.
(Nicht-)Wechselwirkende Kristalle
Viele der alltäglichen Kristalle bestehen auf die eine oder andere Weise aus elektrisch geladenen Ionen, also Atomen, die gegenüber ihrem elektrisch neutralen „Normalzustand“ zu wenig oder zu viele Elektronen haben. Hier sorgt die elektrische Abstoßung gleicher Ladungen dafür, dass die Teilchen – vereinfacht dargestellt – versuchen, ihren gegenseitigen Abstand zu maximieren. Mit diesem relativ einfachen Bild lässt sich die kristalline Struktur vieler Festkörper schon recht gut erklären.
Etwas komplizierter wird es zum Beispiel bei den Kristallen, die als Schnee vom Himmel fallen oder die wir zuhause im Eisfach sehen. Kristallisiertes Wasser, also „Eis“, lässt sich mit dem Bild von geladenen Teilchen auf den ersten Blick nicht erklären – die Wassermoleküle sind elektrisch neutral, wieso sollten sie also kristallisieren? In der Tat ist es so, dass sich auf mikroskopischer Ebene kleine Ungleichheiten in der Ladungsverteilung innerhalb der Moleküle ergeben (Wissenschaftler*innen sprechen von einem Dipolmoment). Diese winzigen elektrischen Ladungen reichen aus, um für das geordnete, sechseckige Muster zum Beispiel in Schneeflocken zu sorgen.
Aber was, wenn die Teilchen tatsächlich nicht miteinander wechselwirken? Was, wenn wir einzelne Atome betrachten, die scheinbar nichts voneinander „spüren“. Können wir trotzdem einen Kristall, also eine räumliche Ordnung, beobachten? Das Heidelberger Experiment zeigt: ja! Obwohl die Atome in diesem Experiment nicht miteinander wechselwirken, also zum Beispiel nicht elektrisch geladen sind, bildet sich auf winzigen Längenskalen ein Kristall, der experimentell beobachtet werden konnte. Aber wie kann das sein?
Das Pauli-Prinzip
Eines der fundamentalen Gesetze der Natur ist das sogenannte Pauli-Prinzip. Um zu verstehen, worum es dabei geht, müssen wir zuerst verstehen, wie sich mikroskopische Teilchen beschreiben lassen.
In der Physik verwenden wir dazu die Quantenmechanik. Dabei ordnen wir einem „Teilchen“ eine sogenannte Wellenfunktion \(\Psi\) zu, die – grob gesagt – beschreibt, wo man das Teilchen mit welcher Wahrscheinlichkeit beobachten kann. Tatsächlich hängt diese Wahrscheinlichkeit sogar nur vom Betrag der Wellenfunktion ab.
Eine wichtige Erkenntnis ist, dass unter bestimmten Situationen zwei quantenmechanische Teilchen in jeder Hinsicht ununterscheidbar sein können. In der Praxis bedeutet das unter anderem, dass sich die Ergebnisse von Messungen nicht ändern, wenn wir die beiden Teilchen austauschen. Auch die Wahrscheinlichkeit, überhaupt ein Teilchen an einem bestimmten Ort zu beobachten, ändert sich also nicht.
Wir können diese beiden Aussagen zusammenführen: Wenn wir zwei Teilchen vertauschen, so darf sich der Betrag der Wellenfunktion nicht ändern. Das heißt, die Wellenfunktion selbst darf sich höchstens durch ein Vorzeichen unterscheiden. Das erlaubt es uns, Teilchen in zwei Kategorien zu unterteilen:
- Bosonen, deren Wellenfunktion sich beim Vertauschen nicht ändert: \(\Psi(2, 1) = \Psi(1, 2)\).
- Fermionen, deren Wellenfunktion beim Vertauschen ein zusätzliches Minus erhält: \(\Psi(2, 1) = -\Psi(1, 2)\).
Wir wollen uns jetzt ununterscheidbare Fermionen etwas genauer ansehen. Dazu wollen wir versuchen, zwei Fermionen am selben Ort zu beschreiben. In diesem Fall ändert sich die Wellenfunktion beim Vertauschen nicht, allein deshalb, weil Vertauschen zweier ununterscheidbarer Teilchen am selben Ort tatsächlich keinen Unterschied macht. Gleichzeitig ändert aber die Wellenfunktion ihr Vorzeichen, weil wir nach wie vor über Fermionen sprechen! Das heißt, wir erhalten für die Wellenfunktion am Ort \(x\), dass \(\Psi(x, x) = -\Psi(x,x)\). Die einzige Möglichkeit, diese Gleichung zu lösen, ist \(\Psi(x,x)=0\). Das heißt, die Wahrscheinlichkeit, zwei Fermionen am selben Ort zu finden, ist Null. Oder in der Sprache des Pauli-Prinzips ausgedrückt:
Zwei Fermionen können sich nicht im selben Quantenzustand befinden.
Pauli-Kristalle
Eine spannende Konsequenz des Pauli-Prinzips ist, dass Fermionen, die nicht miteinander wechselwirken, trotzdem zu „wissen“ scheinen, wenn ein anderes Fermion ihnen sehr nahe kommt. Das hat zum Beispiel zur Folge, dass ununterscheidbare Fermionen, wenn sie einander nahe genug kommen, kristallartige Strukturen formen können, sogenannte Pauli-Kristalle, die einzig durch das Pauli-Prinzip verursacht werden.
Um solche Pauli-Kristalle im Experiment beobachten zu können, müssen die Teilchen einige Eigenschaften erfüllen:
- Die Teilchen müssen sehr langsam sein, damit wir sie verlässlich beobachten können und insbesondere ein klares räumliches Muster messen können.
- Die Teilchen dürfen nicht anderweitig miteinander wechselwirken oder diese Wechselwirkung muss extrem schwach sein. Alle elektrisch geladenen Teilchen scheiden deshalb aus.
- Trotzdem müssen die Teilchen irgendwie zusammengehalten werden, damit sie einander nah genug sind, um einen Effekt des Pauli-Prinzips zu beobachten.
Das Experiment
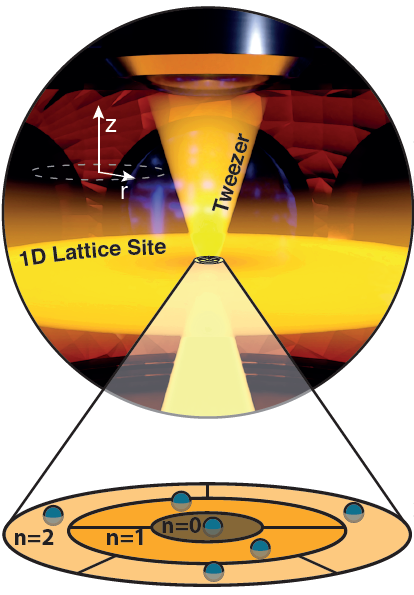
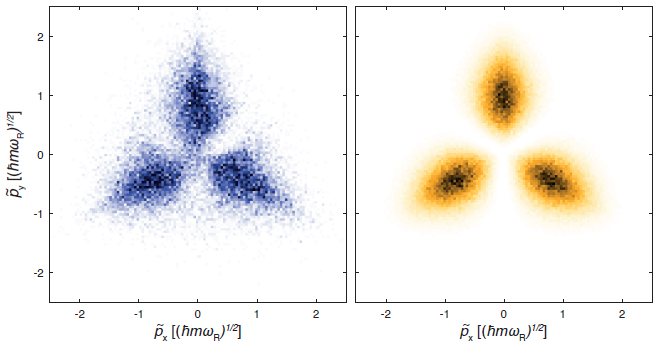
Um diese Voraussetzungen zu erfüllen, haben Wissenschaftler in der Gruppe von Selim Jochim und Philipp Preiss fermionische Lithium-6-Atome mit Lasern auf Temperaturen nahe dem absoluten Nullpunkt gekühlt. Komplexe optische Techniken erlauben es, die Atome einzufangen und im Wesentlichen in einer zwei-dimensionalen Scheibe zu halten. Mit einem weiteren Laser wurden die Atome zum Fluoreszieren gebracht, um ihre Positionen beobachten zu können. Durch wiederholte Messungen zeigt sich schließlich eine charakteristische Verteilung der Teilchenimpulse, einer Größe, die aus den experimentellen Daten abgeleitet werden kann. Diese Verteilung entspricht einer regelmäßigen räumlichen Anordnung – also dem, was wir normalerweise als „Kristall“ kennen. Weil die Impulsverteilung der nicht-wechselwirkenden Teilchen gerade der Vorhersage für Pauli-Kristalle entspricht, können wir tatsächlich von der ersten experimentellen Realisierung dieser exotischen Kristalle sprechen.
Was bedeutet das?
Die Tatsache, dass das Experiment Pauli-Kristalle finden konnte, ist an sich nicht überraschend. Theoretiker hatten schon früher die Existenz von Pauli-Kristallen in solchen Aufbauten vorhergesagt (Rakshit et al., Scientific Report 7, 15004 (2017)). Dennoch ist es jedes Mal wieder sehr erfreulich und beeindruckend, etwas so Fundamentales wie das Pauli-Prinzip erneut bestätigt zu sehen.
Spannend ist auch, dass die quantenmechanische Natur der Teilchen alleine schon ausreicht, um interessante Strukturen – in der Fachsprache „Korrelationen“ – beobachten zu können. Eine natürliche Frage ist jetzt, wie sich diese Korrelationen verändern, wenn die Teilchen miteinander wechselwirken. Auch dazu gibt es natürlich theoretische Vorhersagen und Experimente mit kalten Atomen bieten dafür eine tolle Plattform. Ich bin auf jeden Fall gespannt, was die Kolleg*innen in der Experimentalphysik als nächstes finden!